函数的凹凸区间是什么？

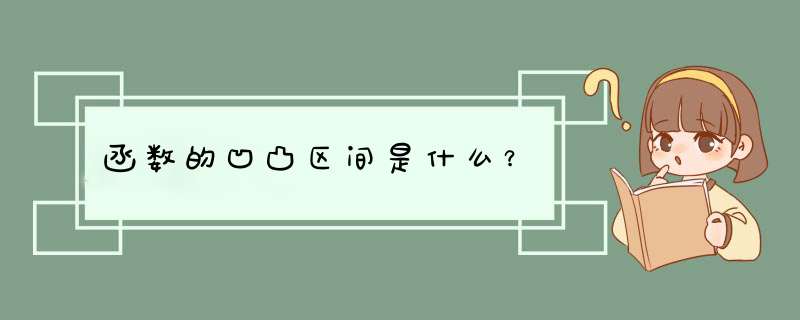
函数的凹凸性的定义：

设函数f(x)在区间I上有定义，若对I中的任意两点x₁和x₂，和任意λ∈(0,1)，都有：

f(λx₁+(1-λ)x₂)>=λf(x₁)+(1-λ)f(x₂)。

则称f为I上的凸函数，若不等号严格成立，即“>”号成立，则称f(x)在I上是严格凸函数。

同理，如果">=“换成“<=”就是凹函数。类似也有严格凹函数。

凹凸函数的判定方法：

1、在图像上任取两点A、B连接，若函数图像在两点间的部分均在直线下方，则把该函数在[A，B]之间的部分定义为凹函数。反正为凸函数。

2、求函数的二阶导函数，f”(X)，若二阶导函数在[A，B]之间，则：

（1）若 f”(X) ≥ 0，原函数为凹函数。

（2）若 f”(X) ≤ 0，原函数为凸函数。

确定曲线y=f(x)的凹凸区间和拐点的步骤：

1、确定函数y=f(x)的定义域。

2、求出在二阶导数f"(x)。

3、求出使二阶导数为零的点和使二阶导数不存在的点。

4、判断或列表判断，确定出曲线凹凸区间和拐点。

1、已知函数表达式，但不容易做出图形是可以利用其二阶导数符号来判定函数的凹凸性

y''>0是凹函数

y''<0是凸函数

2、如果可以从函数的表达式入手做出其草图，也可从图形中判断其凹凸性，开口向下为凸，开口向上为凹。

3、利用曲线与曲线上切线位置关系也可判断函数的凹凸性：切线总是位于曲线上方，则曲线为凸；切线总位于曲线下方，则曲线为凹

看导数,代数上,函数一阶导数为负,二阶导数为正（或者一阶正,二阶负）,便是凸的,一阶与二阶同号为凹．．．．．．．．函数在凹凸性发生改变的点称为拐点,拐点的二阶导数为0或不存在二阶导数

f"(x)>0：图形是向下凹的。

f"(x)<0：图形是向上凸的。

求取函数的一阶导数f'(x)、 二阶导数f"(x)，如果：

f'(x)>0；f"(x)<0：函数图形是单调递增“↗”“上”“凸”的曲线。

f'(x)<0；f"(x)<0：函数图形是单调递增“↘”“下”“凸”的曲线。

f'(x)>0；f"(x)>0：函数图形是单调递增“↗”“上”“凹”的曲线。

f'(x)<0；f"(x)>0：函数图形是单调递增“↘”“下”“凹”的曲线。

综上所述：

f"(x)<0：图形是凸的。

f"(x)>0：图形是凹的。

扩展资料：

函数y=f（x）的导数yˊ=fˊ（x）仍然是x的函数，则y′′=f′′（x）的导数叫做函数y=f（x）的二阶导数。在图形上，它主要表现函数的凹凸性。

如果一个函数f(x)在某个区间I上有f''(x)（即二阶导数）>0恒成立，那么对于区间I上的任意x,y，总有：f(x)+f(y)≥2f[(x+y)/2]，如果总有f''(x)<0成立，那么上式的不等号反向。

如果一个函数f(x)在某个区间I上有f''(x)（即二阶导数）>0恒成立，那么在区间I上f(x)的图象上的任意两点连出的一条线段，这两点之间的函数图象都在该线段的下方，反之在该线段的上方。

--二阶导数

图象可以判断。 

用盛水法则：（形象得要死） 

可以盛水的“凹”啊，（盛水量为正，二阶导数为正），凹函数。如，开口向上的抛物线函数y＝x^2, y'=2x,y''=2>0凹函数 

反之， 

不可以盛水的“凸”啊，（盛水量差点儿为“负”，二阶导数为负），凸函数。如，开口向下的抛物线函数y＝－x^2, y'=－2x,y''=－2<0凸函数 

就像单调性离不开单调区间一样，函数的凸凹性与凸凹区间是分不开的。 

可能在整个定于域上或者是凸的，或者凸的。如上述例子。 

也可能在定义域上凸凹区间相间，如y＝sinx。如图。

函数的凹凸性指的是：函数图象所表现出来的凹凸性，即函数在二元坐标系表现出的性质。如一元二次函数，其解析式可表示为：y=ax^2+bx+c（a≠0）

当a＞0时，二次函数有最小值，所以函数图象表现为凹性，

当a＜0时，二次函数有最大值，所以函数图象表现为凸性。

其函数图象表示如下：

总而言之，函数的凹凸性为函数图象的直观表示。