数据库：求F={A→B,B→A,B→C,A→C,C→A},最小（极小）函数依赖集合

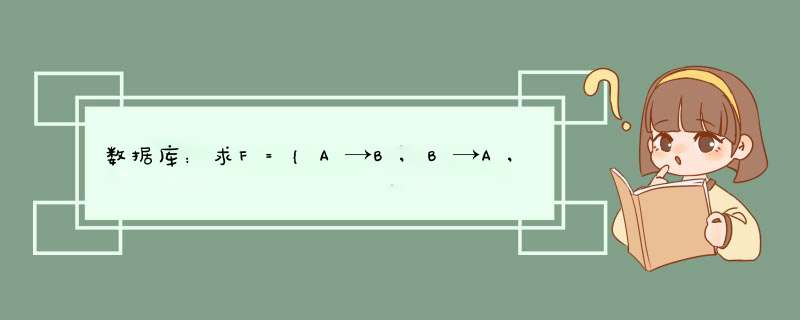
利用分解规则，将所有的函数依赖变成右边都是单个属性的函数依赖。从题目来看，F中的任何一个函数依赖的右部仅含有一个属性：{A→B，B→A，B→C，A→C，C→A}

第二步去冗余的的顺序不同，产生结果也会不同，故最小函数依赖集合不止一个，还可发现另一个最小（极小）函数依赖集合为：{A→B，B→A，A→C，C→A}

给定一个数集A，假设其中的元素为x。现对A中的元素x施加对应法则f，记作f（x），得到另一数集B。假设B中的元素为y。则y与x之间的等量关系可以用y=f（x）表示。函数概念含有三个要素：定义域A、值域C和对应法则f。其中核心是对应法则f，它是函数关系的本质特征。

扩展资料：

函数的对应法则通常用解析式表示，但大量的函数关系是无法用解析式表示的，可以用图像、表格及其他形式表示。

函数与不等式和方程存在联系（初等函数）。令函数值等于零，从几何角度看，对应的自变量的值就是图像与X轴的交点的横坐标；从代数角度看，对应的自变量是方程的解。

另外，把函数的表达式（无表达式的函数除外）中的“=”换成“<”或“>”，再把“Y”换成其它代数式，函数就变成了不等式，可以求自变量的范围。

参考资料来源：百度百科——函数

1.首先把右边的属性都变成单个属性

函数依赖集F={BE→G,BD→G,CD→A,CE→G,CDE→A,CDE→B,BC→A,B→D}

2.对于函数依赖F中的每个函数X->A,设G=F-{X->A},如果A属于关于函数依赖集G的闭包，将X->A从F中删除，否则保留，然后得出新的F。

BE+=BEDG，包含G，删除。

BD+=BD,不包含G，保留。

CD+=CD，不包含A，保留。

CE+=CE，不包含G，保留。

CDE+=CDEAGBA，包含A，删除。

CDE+=CDEAG，不包含B，保留。

BC+=BCDGA,包含A，删除。

B+=B，不包含D，保留。

得到新的F={BD→G,CD→A,CE→G,CDE→B,B→D}

3.对于F中每一个左端包含多个属性的X->A（即去掉各依赖左部多余的属性。一个一个地检查函数依赖左部非单个属性的依赖），选择X的每个子集Z,如果A属于Z的闭包,则用Z->A代替X->A。

BD→G：B+=BDG，包含G，去掉；D+=D，不包含G，保留。

CD→A：C+=C，不包含A，保留；D+=D，不包含A，保留。

CE→G：C+=C，不包含G，保留；E+=E，不包含G，保留。

CDE→B：C+=C，不包含B，保留；D+=DG，不包含B，保留；E+=E，不包含B，保留。

最后得出关系模式R(U,F)的最小依赖集Fm={D→G,CD→A,CE→G,CDE→B,B→D}

1.F={A->B,C->D,AE->F，F->G}已经是F的最小函数依赖集

2.R的候选码：ACE

3.R分解为：R1(A，B，C，D，E)和R2(F,G)均满足BCNF范式

---