设函数f(x)=x-a 的绝对值，g(x)=ax. 1. 当a=2时，解关于x的不等式f(x)＜g(x) 2. F=f(x)-g(x),求函数F(x)在

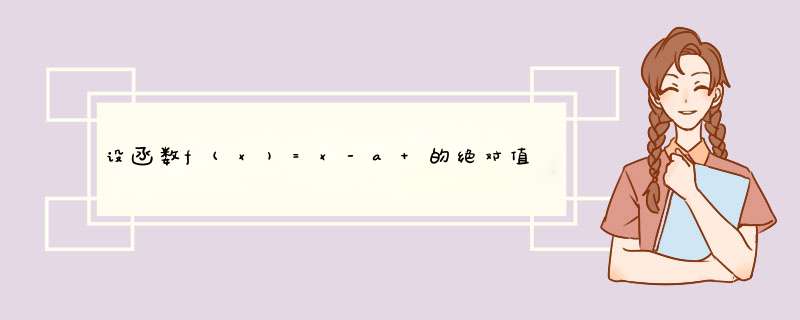
（1）当x>/2时,x-2<2x,解得x>-2（x>2），所以x>/2

当x<2时，-（x-2）<2x，解得 2/3<x<2 （x<2）

综上所述，x>2/3

（2）F=f(x)-g(x)

数形结合：当x=a时,F(x)=f(x)-g(x)=(a-x)-ax取最小值

（注意（0，a]）

fdnjdjhnjkxvjknsdjnv

首先不必求导函数了，f(x)=|x－a|的图像是以x=a为对称轴的折线。

如果说f(x)=|x－a|在(﹣∞,3)上是减函数,那么答案就是a≤3，现在的题设条件是“递减区间”。

f(x)=|x-a|

f(0)=|a| f(1)=|1-a|

最小值为|a|，在区间的左端点取得

a在区间上的话最小值为f(a)=0，

a在区间右边的话f(x)=a-x, 最小值为f(1)=a-1<a=|a|

a在区间左边的话，f(x)=x-a, 最小值为f(0)=-a=|a|

因此a必在区间的左端, 即a<=0